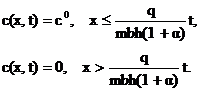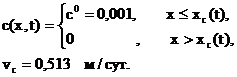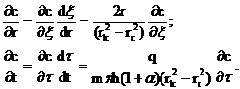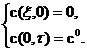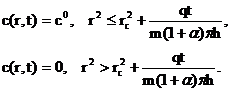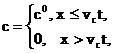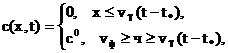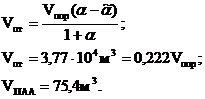добываем нефть и газ

Применение физико-химических методов основывается на вытеснении нефти из пластов растворами различных активных примесей. К таким примесям, улучшающим процесс вытеснения нефти по сравнению с заводнением, относятся поверхностно-активные вещества, полимеры, мицеллообразующие вещества, щелочи, углекислота и др.

При проектировании разработки месторождений нефти с помощью различных физико-химических методов необходимо уметь определять время образования оторочки водного раствора актив­ной примеси и необходимый для ее формирования объем химреагента, скорость продвижения оторочки по пласту, количество адсорбирующегося (т. е. осаждающегося на поверхности породы) химреагента в процессе вытеснения нефти. Кроме того, необходимо оценивать эффективность процесса вытеснения.

Задачи 1—7 посвящены изучению скорости продвижения фронта активной примеси в пласте в случаях прямолинейной и плоско-радиальной фильтрации жидкостей, определению оптималь­ных размеров оторочек активных примесей и времени их создания.

Задача 1. В водонасыщенный участок пласта шириной b = 400 м, толщиной h = 15 м, пористостью т =0,25 и с расстоя­нием между нагнетательной и добывающей галереями l= 500 м через нагнетательную галерею закачивается водный раствор ПАВ с концентрацией c₀ и темпом закачки q = 500 м^з/cyт. ПАВ сорбируется скелетом породы по закону Генри, формула которого имеет вид a(с) = c, где - коэффициент сорбции;

= 0,2.

Определить скорость продвижения фронта сорбции ПАВ (фронта ПАВ) и построить график распределения концентрации ПАВ в пласте в произвольный момент времени.

Р е ш е н и е. Для определения скорости фронта ПАВ и распре­деления их концентрации в пласте выведем уравнение материального баланса. Для этого выделим эле­мент объема пласта (рис.1) =xbh, в котором будем считать движение жидкостей происходящим вдоль оси Ох, и составим уравнение баланса объема ПАВ. Воду и водный раствор ПАВ будем считать несжимаемыми жидкостями.

q h q

b

x

Рис.12. Элемент прямолинейного пласта.

За время t в элемент V войдет объем ПАВ

За то время из элемента V выйдет объем ПАВ

В момент времени t в элементе объема пласта V было ПАВ

За время количество ПАВ изменилось и стало равным

Здесь — некоторая точка интервала , в которой концентрация ПАВ равна среднему значению концентрации в элементе объема V соответственно в моменты времени t и t +t.

Составляя уравнение баланса, получим

или

Деля обе части полученного уравнения на и устремляя и к нулю, получим

Вспоминая, что по условию задачи a(с) = с, и производя несложные преобразования, получим окончательную форму уравнения баланса водного раствора ПАВ в первоначально водонасыщенном пласте:

(1)

Для решения этого уравнения необходимо знать начальные и граничные условия. Сформулируем эти условия.

В начальный момент времени t = 0 в пласте отсутствует ПАВ, т. е.

(2)

Начиная с момента времени t = 0 в пласт через нагнетательную галерею закачивается водный раствор ПАВ с концентрацией закачки с = с⁰ .Таким образом, граничное условие будет иметь вид

(3)

Решение задачи (1)—(3) хорошо известно, результат определяют по формулам

(4)

Отсюда следует, что фронт сорбции ПАВ движется со скоростью

где — линейная скорость фильтрации,

м/сут.

Подставляя в выражение для скорости фронта сорбции ПАВ значение скорости фильтрации v и заданные по условию задачи значения пористости и коэффициента сорбции ПАВ, находим v_c:

0,277 м/сут.

Распределение концентрации ПАВ в пласте вдоль оси Ох в произвольный момент времени t соответствии с формулой (4) имеет вид, изображенный на рис. 13.

с

с⁰

v_c

0 x_c x

Рис.13. Зависимость концентрации ПАВ в случае линейной изотермы

сорбции ПАВ пористой средой от расстояния

Задача 2. В первоначально насыщенный пласт толщиной h=10м и пористостью m= 0,2 через нагнетательную галерею шириной b=300м закачивается водный раствор полиакриламида (ПАА) с концентрацией c⁰=0,001 и темпом закачки q=400 м³/сут. ПАА сорбируется пористой средой по закону Генри (изотерма сорбции Генри).

Найти распределение концентрации ПАА в пласте в любой момент времени tи скорость фронта ПАА v_c (скорость фронта сорбции ПАА). Движение жидкостей считать прямолинейным.

О т в е т:

Задача.3. В водонасыщенный участок пласта, имеющий r_к=200 м и толщину h=10 м и пористость m=0,2, через центральную скважину радиусом r_c=0,1м закачивается водный раствор ПАВ с концентрацией c⁰ и темпом закачки q=250 м³/сут. ПАВ интенсивно сорбируется пористой средой по закону Генри.

Определить закон продвижения фронта ПАВ (фронта сорбции ПАВ) и время подхода его к линии отбора, расположенной на расстоянии r=r_c=200 м от центральной нагнетательной скважины. Движение жидкостей в пласте считать плоско-радиальным, а сами жидкости — несжимаемыми.

Р е ш е н и е. Для определения скорости продвижения фронта ПАВ выведем уравнение, описывающее распределение концентрации ПАВ в пласте. Для этого поступим так же, как и в задаче 1, и выделим элемент объема пласта и рассмотрим баланс ПАВ в этом объеме (рис. 14).

r Dr

h

Рис.14. Схема элемента пласта при плоско-радиальной фильтрации

За время Dt в элемент войдет объем ПАВ

За то же время Dt из элемента через поперечное сечение с координатой r+Dr выйдет объем ПАВ

В момент времени t в элементе объема пласта DV содержалось ПАВ

За время Dt количество ПАВ изменилось и стало равным

Здесь — некоторая точка между сечениями r и , в которой концентрация равна среднему значению концентрации в выделенном нами элементе объема соответственно в моменты времени t и .

Составляя уравнение баланса, получим

или

Деля обе части полученного уравнения на DVDt и устремляя Dr и Dt нулю, получим (замечая, что при )

или с учетом того, что a(с) = с,

(5)

Это и есть дифференциальное уравнение баланса концейтрации ПАВ в водонасыщенном пласте.

Для его решения необходимо знать начальные и граничные условия. Сформулируем их. В начальный момент времени в пласте отсутствует ПАВ, т. е.

(6)

Начиная с момента времени t=0 в пласт закачивается водный раствор ПАВ с концентрацией c=c⁰. Поэтому граничное условие имеет вид

(7)

С помощью замены переменных

(8)

приведем условия задачи (5)-(7) к более удобному для решения виду. Вычисляя производные, входящие в уравнение (5), последовательно получим

Подставляя полученные соотношения в уравнение (5), будем иметь

(9)

Начальные и граничные условия примут вид

(10)

Решение задачи (9)—(10) хорошо известно и имеет вид

т. е. положение фронта ПАВ определяем с помощью уравнения

Переходя к размерным величинам, получим

Таким образом, положение фронта ПАВ можно определить по соотношению

(11)

Дифференцируя обе части уравнения (11) по t найдем скорость продвижения фронта ПАВ

(12)

Таким образом, скорость продвижения фронта ПАВ в случае плоско-радиальной фильтрации падает с течением времени по закону, формула которого имеет вид (12).

Найдем время подхода фронта ПАВ к линии отбора. Для этого подставим в соотношение (11) значение и, возведя обе части полученного равенства в квадрат, найдем

Задача 4. В семиточечный элемент пласта площадью S=100 000 м ² через центральную скважину закачивается водный раствор ПАВ с концентрацией с⁰ при темпе закачки q =500 м³/сут. ПАВ адсорбируется пористой средой по закону Генри

а(с)= ,

где а – константа Генри, равная 0,25. Толщина пласта h= 15 м, пористость m=0,25. Пласт полностью насыщен водой.

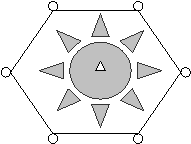Рис.15. Семиточечный элемент пласта

Определить время подхода фронта ПАВ к добывающим скважинам, а также скорость продвижения этого фронта в начальный и конечный моменты времени. Движение жидкостей считать плоско-радиальным, а сами жидкости — несжимаемыми.

У к а з а н и е. За время подхода фронта ПАВ к добывающим скважинам (т. е. в конечный момент времени t*) считать время, к которому площадь круга, ограниченная фронтом ПАВ, будет равна площади семиточечного элемента.

О т в е т:

t*= 2,57 года; = 170 м/сут; =3м/сут.

Задача 5. В пласт, первоначально насыщенный водой с пористостью т = 0,2 и имеющий размеры l = 500 м, b= 300 м , h= 10 м, закачивается оторочка ПАВ с концентрацией с° = 0,001 при расходе q = 400 м³/сут. Оторочка проталкивается водой с тем же расходом q. ПАВ адсорбируется пористой средой по закону, формула которого имеет вид

На стадии проталкивания оторочки водой происходит десорбция ПАВ (т. е. обратное растворение части адсорбированного ПАВ в прокачиваемой воде).

где характеризует необратимо сорбированное породой количество ПАВ (рис. 16).

а(с)

2

а₀ 1

0 с₀ с

Рис. 16. График зависимости сорбции (1) и десорбции (2) ПАВ пористой породой (случай линейной изотермы сорбции и десорбции); а₀ – количество ПАВ, необратимо сорбированного породой.

Определить оптимальный объем оторочки ПАВ и время, необходимое для ее создания. Оптимальным считать такой объем оторочки, который исчезает при подходе фронта ПАВ к линии отбора. Движение жидкостей считать прямолинейным, а сами жидкости — несжимаемыми.

Р е ш е н и е. На стадии создания оторочки ПАВ решение известно (см. задачу 1):

где

Будем считать, что в момент времени t=t_* формирование оторочки закончилось и началась стадия проталкивания ее по пласту водой, закачиваемой с расходом q. Для определения скорости тыла оторочки ПАВ выведем уравнение, описывающее распределение

концентрации активных веществ на стадии проталкивания оторочки закачиваемой водой.

Выделим элемент объема пласта (см. рис. 12) и рассмотрим баланс объема ПАВ.

За время в элемент вошел объем ПАВ

За это же время из элемента вышло следующее количество ПАВ:

В момент времени t в элементе объема содержалось количество ПАВ

которое за время изменилось и стало равным

Составляя уравнение баланса, получим

или после подстановки полученных выражений для Q₁-Q₄ деления обеих частей уравнения на и устремления и к нулю будем иметь

Используя выражение для определения после несложных преобразований получим уравнение распределения концентрации ПАВ в пласте на стадии проталкивания оторочки водой в виде

(13)

Отметим, что в момент времени (момент окончания создания оторочки и начала проталкивания ее водой) во всех сечениях пласта, через которые прошел фронт оторочки ПАВ, концентрация ПАВ будет равна концентрации закачки. Таким образом, начальное условие будет иметь вид

(14)

Начиная с момента времени t=t_* оторочка будет проталкиваться водой, не содержащей ПАВ. Поэтому граничное условие примет вид

(15)

Решение задачи (13)—(15) хорошо известно. Результат получают по формулам

c

c₀

0 х_T(t) х_ф(t) x

Рис. 17. Зависимость концентрации ПАВ в пласте при проталкивании оторочки раствора водой (случай линейных изотерм сорбции и десорбции ПАВ) от расстояния. Движение прямолинейно-параллельное:

c — концентрация ПАВ, x_ф и х_T ответственно положение фронта и тыла оторочки ПАВ в момент времени t

где - скорость тыла оторочки, определяемая по соотношению

Характерное распределение концентрации ПАВ в пласте показано на рис. 17.

Найдем время создания оторочки. Из определения оптимального объема оторочки имеем

Решая эти два уравнения относительно , получим

Объем оторочки ПАВ при этом составит

Таким образом, для условий нашей задачи оптимальным является объем оторочки ПАВ, равный 15 % порового объема пласта .

Задача 6. В водонасыщенный пласт толщиной h =5 м и пористостью т = 0,27 через нагнетательную скважину радиусом r_c = 0,1м, расположенную в центре пласта, закачивается оторочка водного раствора полиакриламида (ПАА) концентрацией c0= 0,002 при расходе q = 250 м³/сут. По окончании создания оторочки она проталкивается по пласту водой, закачиваемой в нагнетательную скважину с тем же расходом q. ПАА адсорбируется пористой средой по закону, формула которого имеет вид

На стадии проталкивания оторочки ПАА водой происходит десорбция полиакриламида по закону, формула которого имеет вид

где = 0,05 — коэффициент десорбции; необратимо сорбированное породой количество полиакриламида.

Отбор жидкости производится через добывающую галерею, расположенную на расстоянии r_к= 200 м от центра нагнетательной скважины.

Вывести формулу для расчета оптимального объема оторочки ПАА и определить объем оторочки и количество ПАА, необходимое для создания такой оторочки.

У к а з а н и е. Пользуясь решениями, приведенными в задачах 3 и 5, получить выражения для скоростей движения фронта и тыла оторочки ПАА.

О т в е т:

Задача 7. Определить время t_* закачки в пласт водного раствора полиакриламида (ПАА) для создания оторочки ПАА оптимального объема. Условия задачи те же, что и задачи 6.

О т в ет: t_*= 203,6 сут.

Tags: Расчет фильтрация водных растворов активных примесей в пласте

This entry was posted on Понедельник, Апрель 18th, 2011 at 7:52 пп and is filed under Расчет фильтрация водных растворов активных примесей в. You can follow any responses to this entry through the RSS 2.0 feed. Both comments and pings are currently closed.